S pomočjo metode Monte Carlo lahko izračunamo približek ploščine prerešetanega vala. Slednjega dobimo tako, da iz ploščice 1m x 3m najprej izrežemo sinusni val in nato zvrtamo n lukenj.
Program, s katerim bomo računali približek ploščine prerešetanega vala:

Kaj predstavljajo posamezne spremenljivke:

Program uporabimo za reševanje vseh podnalog.
PREREŠETANI VAL
Python: Po 10.000.000-ih poskusih (točkah) je približek ploščine prerešetanega vala enak 1,3163706.

GeoGebra: Grafičen prikaz prerešetanega vala.

WolframAlpha: Izračun ploščine prerešetanega vala s pomočjo integrala = 1,31644.

Primerjava: Python: 1,3163706 | Wolfram: 1,31644
DEL LUKNJE IZVEN SINX
Python:

GeoGebra:
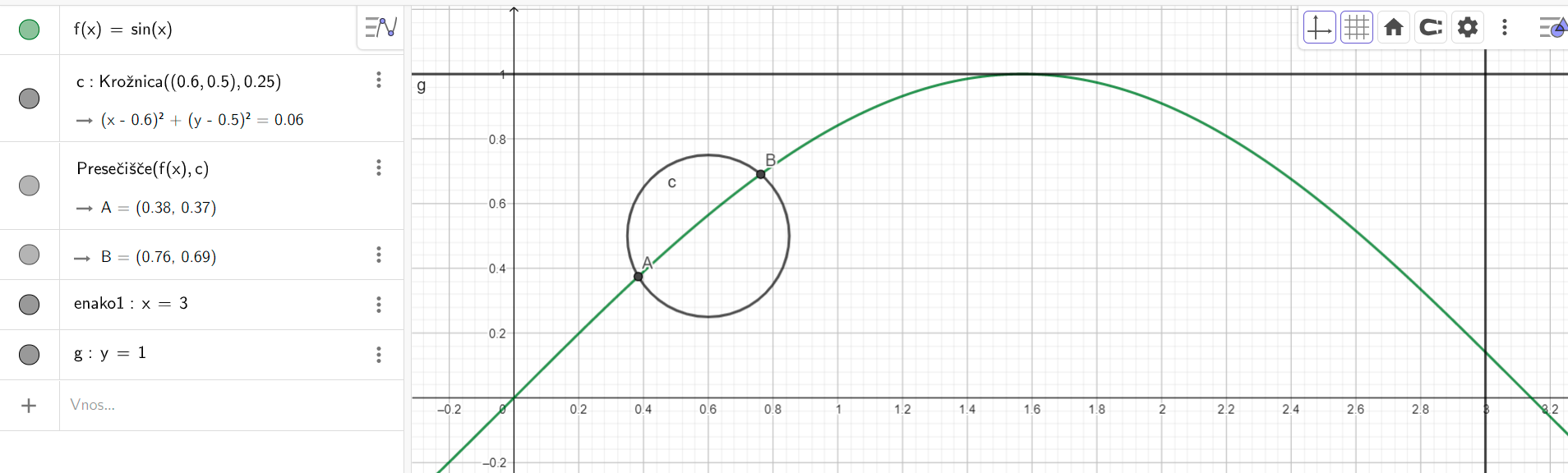
Za lažji izračun krivulji premaknemo tako, da ima krog središče v koordinatnem izhodišču.

Sinusni val in krožnica z novo enačbo. Označene točke predstavljajo meje integrala.

Najprej izračunamo ploščino lika ABC.

Nato še ploščino lika ACD.

Za lažjo predstavo lahko krivulje zrcalimo čez x os.

WolframAlpha:
Ploščina prvega območja:

Ploščina drugega območja:

Ploščina prerešetanega vala:

Primerjava: Python: 1,8686625 | Wolfram: 1,86838
LUKNJI SE PREKRIVATA
Python:

GeoGebra:

Za lažji izračun krožnici premaknemo tako, da ima ena od njiju središče v koordinatnem izhodišču.

Krožnici z novo enačbo. Označene točke predstavljajo meje integrala.

WolframAlpha:
Ploščina desnega koščka:

Ploščina levega koščka:

Ploščina prerešetanega vala:

Primerjava: Python: 1,379802 | Wolfram: 1,37962
DEL LUKNJE IZVEN SINX IN LUKNJI SE PREKRIVATA
Python:

GeoGebra:

Za lažji izračun krožnici premaknemo tako, da ima ena od njiju središče v koordinatnem izhodišču.

Krožnici z novo enačbo. Označeni točki predstavljata meje integrala.

WolframAlpha:
Glej: DEL LUKNJE IZVEN SINX


Glej: LUKNJI SE PRIKRIVATA

Ploščina prerešetanega vala:

Primerjava: Python: 1,7515722 | Wolfram: 1,7488